AVL樹的原理與BST原理大致相同,主要目的是讓樹的左右子樹達到平衡;
兩邊的高度差不超過1(平衡),即為AVL樹。
平衡左右子樹的時機,在新增結點後,需檢查樹是否平衡,
不平衡,即進行左旋轉或右旋轉。
package utitled;
public class AVLTreeDemo {
public static void main(String[] args) {
int[] array = {10,11,7,6,8,9};
AVLTree avlTree = new AVLTree();
for (int i = 0; i < array.length; i++) {
avlTree.insertNode(array[i]);
}
System.out.println("====進行平衡後===");
System.out.println("avlTree.getRoot() = " + avlTree.getRoot());
System.out.println("avlTree的高度 = " + avlTree.getRoot().height());
System.out.println("avlTree左子樹高度 = " + avlTree.getRoot().leftHeight());
System.out.println("avlTree右子樹高度 = " + avlTree.getRoot().rightHeight());
avlTree.inOrder();
}
}
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
public void insertNode(int no) {
if (root != null) {
root.insertNode(no);
} else {
root = new Node(no);
}
}
public void deleteNode(int no) {
if (root != null) {
root.deleteNode(no);
}
}
public void inOrder() {
if (root != null) {
root.inOrder();
}
}
}
class Node {
private int no;
private Node left;
private Node right;
private Node parent;
public Node(int no) {
this.no = no;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public Node getParent() {
return parent;
}
public void setParent(Node parent) {
this.parent = parent;
}
@Override
public String toString() {
final StringBuilder sb = new StringBuilder("Node{");
sb.append("no=").append(no);
sb.append('}');
return sb.toString();
}
/**
* 取得樹的高度
* @return
*/
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
/**
* 取得左子樹的高度
* @return
*/
public int leftHeight() {
return left == null ? 0 : left.height();
}
/**
* 取得右子樹的高度
* @return
*/
public int rightHeight() {
return right == null ? 0 : right.height();
}
/**
* 左旋轉
*/
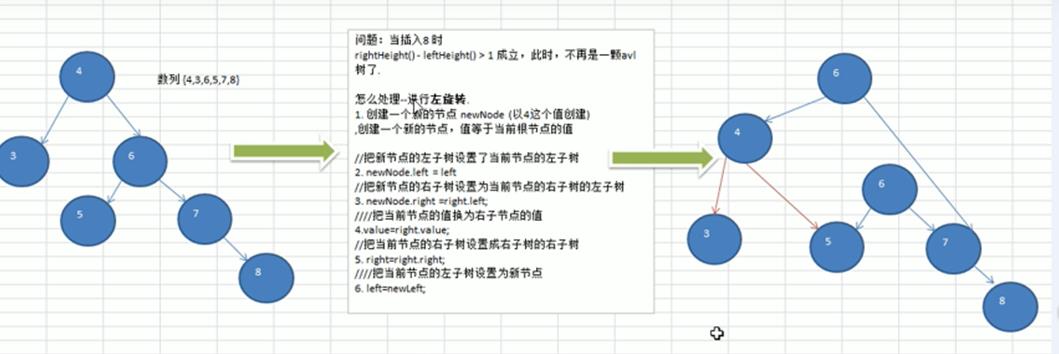
private void leftRotate() {
// 1.創建一個新的結點newNode等於當前根結點的值
Node newNode = new Node(no);
// 2.把新結點的左子樹設置當前結點的左子樹
newNode.left = left;
// 3.把新結點的右子樹設置當前結點的右子樹的左子樹
newNode.right = right.left;
// 4.把當前結點的值換為右子結點的值
no = right.no;
// 5.把當前結點的右子樹設置成右子樹的右子樹
right = right.right;
// 6.把當前結點的左子樹設置為新結點
left = newNode;
}
private void rightRotate() {
// 1.創建一個新的結點newNode等於當前根結點的值
Node newNode = new Node(no);
// 2.把新結點的右子樹設置當前結點的右子樹
newNode.right = right;
// 3.把新結點的左子樹設置為當前結點的左子樹的右子樹
newNode.left = left.right;
// 4.把當前結點的值換為左子結點的值
no = left.no;
// 5.把當前結點的左子樹設置成左子樹的左子樹
left = left.left;
// 6.把當前結點的右子樹設置為新結點
right = newNode;
}
/**
* 查找:找到目標結點與紀錄父結點
* 二叉排序樹的查找是指在二叉排序樹中查找到對應的值,如在上述的二叉排序樹中查找“49”,其具體過程為:
*
* 與根結點的值相比:49<52,查找其左子樹
* 49<58,查找其左子樹
* 49>47,查找其右子樹
* 49<51,查找其左子樹
* 49=49,查找成功
* @param current
* @param no
* @return
*/
public Node searchTarget(Node current, int no) {
if (current == null) {
// 找不到目標結點
return null;
}
if (no == current.getNo()) {
// 找到目標結點
return current;
} else if (no < current.getNo()) {
// 紀錄父結點
parent = current;
// 查找左子樹
return searchTarget(current.getLeft(), no);
} else {
parent = current;
// 查找右子樹
return searchTarget(current.getRight(), no);
}
}
/**
* 插入
* 對於插入操作,主要分為兩種情況:
*
* 若二叉排序樹中存在該值,則不做任何操作
* 若二叉排序樹中不存在該值,則插入
* 插入的具體操作是判斷與二叉排序樹中節點的值,若小於當前節點的值,則選擇左子樹插入,若大於當前節點的值,則選擇右子樹插入;對於左右子樹,進行同樣的操作。
* @param no
*/
public void insertNode(int no) {
Node current = this;
parent = current;
Node temp = null;
if (searchTarget(current, no) == null || searchTarget(current, no).getNo() != no) {
// 查找樹中並不存在no
temp = new Node(no);
if (current == null) {
// 樹為空
current = temp;
} else {
if (no < parent.getNo()) {
// 插入左子樹
parent.setLeft(temp);
} else {
// 插入右子樹
parent.setRight(temp);
}
}
// 右子樹高度 - 左子樹高度 > 1,進行左旋轉
if (rightHeight() - leftHeight() > 1) {
// 若當前結點的右子樹的children: left side height > right side height
// 就先對當前結點的右子樹,進行右旋轉
if (right != null && right.leftHeight() > right.rightHeight()) {
right.rightRotate();
}
// 若上述if-clause不成立就直接對當前結點,進行左旋轉
leftRotate();
}
// 左子樹高度 - 右子樹高度 > 1,進行右旋轉
if (leftHeight() - rightHeight() > 1) {
// 若當前結點的左子樹的children: right side height > left side height
// 就先對當前結點的左子樹,進行左旋轉
if (left != null && left.rightHeight() > left.leftHeight()) {
left.leftRotate();
}
// 上述if-clause不成立就直接對當前結點,進行右旋轉
rightRotate();
}
}
}
/**
* 首先,通過查找二叉排序樹中是否存在節點,若存在,主要分為如下的三種刪除情況
* 1. 節點既無左子樹,又無右子樹:設置父節點指向該節點的指針為空,直接刪除該節點
* 2. 刪除的節點只包含左子樹或者只包含右子樹:刪除該節點,以其左子樹或者右子樹代替該節點
* 3. 刪除的節點既包含左子樹,又包含右子樹:找到待刪除的節點,選擇其左子樹中的最大的節點或者其右子樹中最小的節點,替代待刪除的結點
* @param no
*/
public void deleteNode(int no) {
int side = 0;
// 判斷樹中是否存在no
// 將parent指向待刪除結點的父結點
Node current = this;
parent = current;
if (searchTarget(current, no) != null && searchTarget(current, no).getNo() == no) {
// 樹中存在該結點
// 開始刪除
Node temp = null; // 指向待刪除的結點
if (no < parent.getNo()) {
temp = parent.getLeft();
side = 0;
} else if (no > parent.getNo()) {
temp = parent.getRight();
side = 1;
}
// ===========================================
// 葉子結點,直接刪除
if (temp.getLeft() == null && temp.getRight() == null) {
if (no < parent.getNo()) {
parent.setLeft(null);
} else {
parent.setRight(null);
}
} else if ((temp.getLeft() == null && temp.getRight() != null) || (temp.getLeft() != null && temp.getRight() == null)) {
// 只有左子樹或只有右子樹
Node child = (temp.getLeft() == null ? temp.getRight() : temp.getLeft()); // child指向不為空的子樹
if (no < parent.getNo()) {
parent.setLeft(child);
} else {
parent.setRight(child);
}
} else {
// 既有左子樹又有右子樹
Node childParent = temp.getLeft();
// 這裡選擇左子樹最大的結點作為父結點
// 判斷child的右子樹是否為空
if (childParent.getRight() == null) {
if (side == 0) {
parent.setLeft(childParent);
} else {
parent.setRight(childParent);
}
childParent.setRight(temp.getRight());
} else {
Node maxNodeAtLeft = childParent;
// 尋找右子樹
while (maxNodeAtLeft.getRight() != null) {
maxNodeAtLeft = maxNodeAtLeft.getRight();
}
// 此時maxNodeAtLeft不可能存在右子樹
if (maxNodeAtLeft.getLeft() != null) {
// maxNodeAtLeft存在左子樹
childParent.setRight(maxNodeAtLeft.getLeft());
}
parent.setLeft(maxNodeAtLeft);
maxNodeAtLeft.setLeft(childParent);
maxNodeAtLeft.setRight(temp.getRight());
}
}
// 將待刪除結點設null
temp = null;
}
}
/**
* 中序遍歷
*/
public void inOrder() {
if (this.left != null) {
this.left.inOrder();
}
System.out.println("this = " + this);
if (this.right != null) {
this.right.inOrder();
}
}
}如有敘述錯誤,還請不吝嗇留言指教,thanks!
