線性方程式,高斯消去法
高斯消去法的基本原理
AX=B
其中,A為係數矩陣,X為變數列矩陣,B為常數列矩陣。
假設方程組有equnum方程式個數、有varnum未知個數
我們可以將係數矩陣A和常數列矩陣B,組合成一個廣域矩陣A',在對矩陣中的每一個元素進行消去去操作。
請參閱:演算法筆記- Linear Equation
求解:
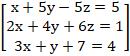
class Program
{
static readonly int MaxNum = 10;
static int[,] ary = {{1,2,-5,5},
{2,4,6,1},
{3,1,7,4}};
static int[] un_result = new int[MaxNum];
static void Main(string[] args)
{
//高斯消去法
//線性方程式
int i, type;
int equnum, varnum;
int[] result = new int[MaxNum]; //儲存方程式的解
equnum = 3; //方程式個數
varnum = 3; //未知數個數
type = GaussFun(equnum, varnum, result);
if (type == -1) //無解
{
Console.WriteLine("該方程式無解!\n");
}
else if (type == -2) //只有浮點數解
{
Console.WriteLine("該方程式只有浮點數解,無整數解!\n");
}
else if (type > 0) //無窮多解
{
Console.WriteLine(string.Format("該方程式有無窮多解!自由變數量為{0}\n", type));
for (i = 0; i < varnum; i++)
{
if (un_result[i] != 0) //判斷不確定變數
{
Console.WriteLine(string.Format("x{0}是不確定的\n", i + 1));
}
else //輸出一組解
{
Console.WriteLine(string.Format("x{0}:{1}\n", i + 1, result[i]));
}
}
}
else //唯一解
{
Console.WriteLine("該方程式的解為:\n");
for (i = 0; i < varnum; i++)
{
Console.WriteLine(string.Format("x{0}:{1}\n", i + 1, result[i]));
}
}
Console.ReadLine();
}
#region 高斯消去演算法
static int GaussFun(int equ, int var, int[] result)
{
int i, j, k;
int col = 0;
int max;
int temp, un_x_num, un_index = 0;
int nu1, nu2;
int gcdtmp, lcmtmp; //利用遞迴求GCD(最大公因數)與LCM(最小公倍數)
int ta, tb;
for (k = 0; k < equ && col < var; k++, col++) //迴圈處理每一行
{
max = k; //儲存絕對值最大的行號
for (i = k + 1; i < equ; i++)
{
if (Math.Abs(ary[i, col]) > Math.Abs(ary[max, col]))
{
//儲存絕對值最大的行號
max = i;
}
}
if (max != k)
{
for (j = k; j < var + 1; j++) //當前列左側為0,交換當前右側資料
{
temp = ary[k, j];
ary[k, j] = ary[max, j];
ary[max, j] = temp;
}
}
if (ary[k, col] == 0) //如果col列第k行以下是0,則處理目前行的下一列
{
k--;
continue;
}
for (i = k + 1; i < equ; i++) //尋找消去的行
{
if (ary[i, col] != 0)
{
nu1 = Math.Abs(ary[i, col]);
nu2 = Math.Abs(ary[k, col]);
while (nu2 != 0) //輾轉相除求最大公因數
{
temp = nu2;
nu2 = nu1 % nu2;
nu1 = temp;
}
gcdtmp = nu1;
lcmtmp = (Math.Abs(ary[i, col]) * Math.Abs(ary[k, col])) / gcdtmp;
ta = lcmtmp / Math.Abs(ary[i, col]);
tb = lcmtmp / Math.Abs(ary[k, col]);
if (ary[i, col] * ary[k, col] < 0) //如果符號不相符
{
tb = -tb; // 異號兩邊相加
}
for (j = col; j < var + 1; j++) //迴圈消去
{
ary[i, j] = ary[i, j] * ta - ary[k, j] * tb;
}
}
}
}
for (i = k; i < equ; i++) //判斷最後一行,最後一列
{
if (ary[i, col] != 0) //若不等於0 表示無解
{
return -1;
}
}
if (k < var) //不確定的變數至少有 VAR-K 個
{
for (i = k - 1; i >= 0; i--) //權圈處理非零行
{
un_x_num = 0; //判斷該行不確定變數的數量
for (j = 0; j < var; j++)
{
if (ary[i, j] != 0 && un_result[j] != 0) //不確定變數判斷
{
un_x_num++; //不確定變數+1
un_index = j;
}
}
if (un_x_num > 1)
{
continue; //若超過一個無法求解
}
temp = ary[i, var];
for (j = 0; j < var; j++)
{
if (ary[i, j] != 0 && j != un_index)
{
temp -= ary[i, j] * result[j];//每次剪去前一係數及解的積
}
}
result[un_index] = temp / ary[i, un_index]; //求出變數
un_result[un_index] = 0; //該變數是確定的
}
return var - k; //自由變數有Var -K
}
for (i = var - 1; i >= 0; i--) //求解
{
temp = ary[i, var];
for (j = i + 1; j < var; j++)
{
if (ary[i, j] != 0)
{
temp -= ary[i, j] * result[j]; //每次減去前一項係數及解的積
}
}
if (temp % ary[i, j] != 0) //如不能整除
{
return -2; //傳回有浮點數解、但無整數解
}
result[i] = temp / ary[i, i];
}
return 0; //唯一解
}
#endregion
}
水滴可成涓流,涓流可成湖泊大海。
汲取累積知識,將知識堆積成常識;將常識探究成學識;將學識簡化為知識;授人自省。