炎龍牙

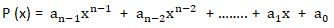
我們稱為P為n次多項次
其表示方法是一個n+2長的陣列，依指數大小儲存，
陣列的第一個元素是代表最大的指數，如

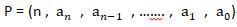
例如多項式
 

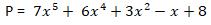
我們可以得到的表示法為P = ( 5 , 7 , 6 , 0 , 3 , -1 , 8 )
由此可以知道運算式取決於 x的指數與係數。

 

        static double polynomial1D(double[] a, int n, double x)
        {
            int i;
            double result;
            result = a[n - 1];
            for (i = n - 2; i >= 0; i--) //遞推演算法計算
            {
                result = result * x + a[i];
            }
            return result;
        }

        static void Main(string[] args)
        {
            //一元多項式
            //建構多項式
            //計算多項次的值
            // P =  7x^5 + 6x^4 + 3x^2 + x + 8
            int i;
            double[] a = { -8.0, 1.0, 3.0, 0.0, 6.0, 7.0 }; //運算式將從常數從最後往前列。
            double x = 0.0;
             double result;
            //想計算的x值
            Console.Write("請輸入x的值：");
            x = Convert.ToDouble(Console.ReadLine());
            
            Console.WriteLine("計算 7x^5 + 6x^4 + 3x^2 + x - 8 的值");
            result = polynomial1D(a,a.Length,x);

            Console.WriteLine("x = {0} 時, P(x) = {1}",x,result);
            Console.ReadLine();
        }

二維多項次
二維多項次求值即計算在指定的(x,y)處的函數值。

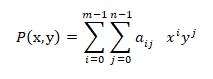
  static double polynomial2D(double[,] a, int m, int n, double x, double y)
        {
            int i, j;
            double result, temp, tt;
            result = 0.0;
            tt = 1.0;
            for (i = 0; i < m; i++) //遞推演算法計算
            {
                temp = a[i, n - 1] * tt;
                for (j = n - 2; j >= 0; j--)
                {
                    temp = temp * y + a[i, j] * tt;
                }

                result += temp;
                tt *= x;
            }
            return result;
        }

        static void Main(string[] args)
        {
            //一元多項式
            //建構多項式
            //計算多項次的值
            // P =  7x^5 + 6x^4 + 3x^2 + x + 8

            double x = 0.0;
            double y = 0.0;
            double result;

            double[,] a = {{1.0,2.0,3.0,4.0,5.0},
                          {6.0,7.0,8.0,9.0,10.0},
                          {11.0,12.0,13.0,14.0,15.0},
                          {16.0,17.0,18.0,19.0,20.0}
                           }; //運算式將從常數從最後往前列。

            //想計算的x值
            Console.Write("請輸入x的值：");
            x = Convert.ToDouble(Console.ReadLine());

            Console.Write("請輸入y的值：");
            y = Convert.ToDouble(Console.ReadLine());

            Console.WriteLine("計算二維多項式的值\n");
            result = polynomial2D(a, a.GetLength(0), a.GetLength(1), x, y);

            Console.WriteLine("x = {0} 時,y = {1} 時, P({0},{1}) = {2}", x, y,result);
            Console.ReadLine();
        }

水滴可成涓流，涓流可成湖泊大海。
汲取累積知識，將知識堆積成常識；將常識探究成學識；將學識簡化為知識；授人自省。