函數,簡單來說,就是「你給我輸入,我給你輸出」,給予數據、資料的輸入,轉換成所需的結果,是解決問題的好工具。在此將以不同的視角來讓您理解函數的功能,並瞭解函數是如何在不同領域協助人們提高工作效率和精確度。對函數多一點認識,就能夠發現函數在職場中的實際價值。
函數的應用也非常宏觀,在不同領域中扮演著不同的角色,然而其核心概念與使用邏輯仍是一致的。想像在數學裡,函數就像一條清楚指引輸入與輸出的路線圖;在物理裡,函數幫助我們了解自然界的運作規則。而在工作相關的領域,如電腦科學裡,函數是一種非常有效率的方式,用來組織資料和解決複雜任務;在程式設計中,函數提升了程式碼的結構性與可重複使用性;而在應用軟體裡,函數更像是你的隱形小助手、小精靈,幫你輕鬆完成各種日常工作。
1. 在數學中(Mathematics)的函數
函數(Function)這一詞,在數學中正是一種映射關係,描述輸入與輸出的對應。例如:
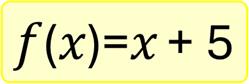
這個函數包含一個輸入變量x,也就是參數x,在此函數的計算式描述了一個映射關係:每當我們輸入一個數值x,函數會將這個數值加上5,然後傳回運算結果。因此,當x為1時,此函數的結果為6。當x為5時,此函數的結果為10。
再譬如下列的函數是一個簡單的二次函數:
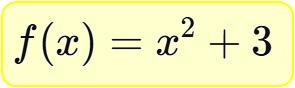
當x的值輸入「2」,函數的結果值便輸出為「7」
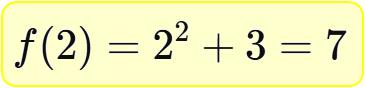
至於複雜一點的數學公式,譬如:包含兩個參數(變數)的方程式:
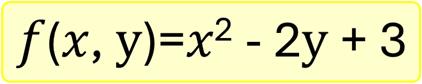
則是包含兩個輸入變化的函數,也就是參數x與參數y。此函數的運算式是參數x值的平方減去2倍的參數y值後再加3,最後傳回運算結果值。所以,當x為2、y為3時,此函數的結果為1。
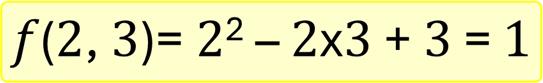
當x為3、y為2時,此函數的結果為8。
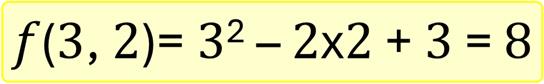
2. 物理中(Physics)的函數
物理學中,函數用來描述變數如何隨時間或條件變化。例如:自由落體運動。自由落體運動是指物體僅在重力作用下垂直下落的運動,若忽略空氣阻力時,加速度等於重力加速度𝑔 ≈ 9.8 m/s²(在地球表面)。其公式如下:
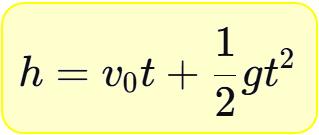
其中,
- ℎ 是物體的下落高度
- 𝑣0代表物體的初速度,若沒有初速度,此值即為0
- 𝑡 代表的是時間(秒)
- 𝑔 代表的是重力加速度
若物體是靜止的,沒有初速度,則公式簡化為:
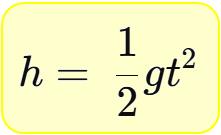
因此,若一個物體自由落體2秒,則透過上述的公式邏輯,我們可以建立一個可運算下落距離的函數為:
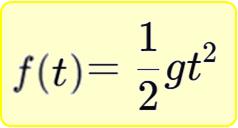
所以,秒數為帶入函數的參數,在帶入2,即表示個物體自由落體2秒,函數便運算出下落距離為:
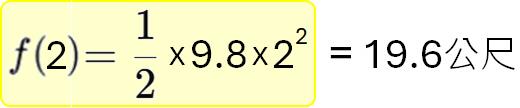
帶入不同的秒數,自然就可以透過相同的邏輯與運算,而輸出不同的結果(高度)囉!我們再另舉一例,若將下落距離規劃為參數,想要計算出物體指定高度自由落下時所需的時間,則此運算時間的函數便可以寫成(此時高度即為參數):
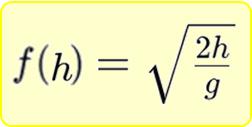
例如:物體從 45 m 高度自由落下,則參數高度帶入函數後,便可運算出落地時間為:

舉一反三,我們可以瞭解到力與加速度的關係(牛頓第二運動定律),或者簡諧運動裡的彈簧振盪、單擺運動,以及電磁學中的庫侖定律(靜電力)、 電磁感應定律(法拉第定律)、...都是物理領域中的函數實例。
3. 電腦科學中的函數(Computer Science)
在電腦科學領域中,函數是一個接收輸入並返回輸出的演算法或程序,通常用於模組化程式設計,以提高程式的可讀性和可重用性。例如:遞迴函數(Recursive Function)可以調用自身的函數,常用於分解問題或樹狀結構搜尋,譬如最有名的費波那契數列(Fibonacci Sequence),這是由義大利數學家萊昂納多·費波那契(Leonardo Fibonacci)引入的數學序列。此序列中的每一個數字都是前兩個數字的和,從而形成了一個無限長的數列。它的起始元素通常是 0 和 1。因此,費波那契數列為:
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,….
其表達式如下:
F (n) = F (n-1) + F (n-2) 其中:
𝐹(0)=0
𝐹(1)=1
以下便是可以輸入一個整數參數n,輸出前n項費波那契數列的函數之虛擬碼(pseudocode):
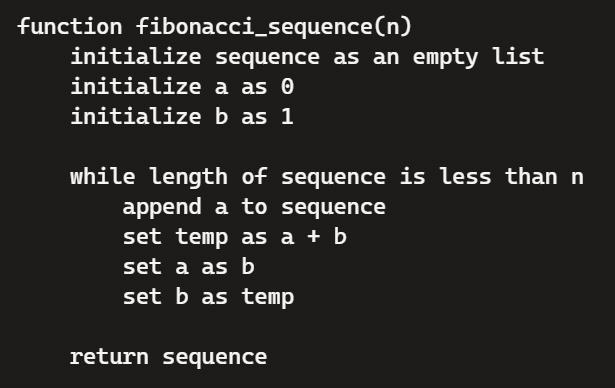
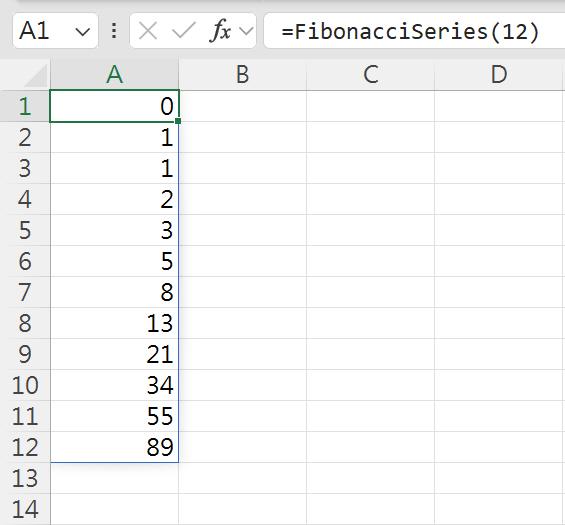
若是在Excel環境裡根據上述的虛擬碼,可以撰寫一個自訂函數來呈現費波那契數列的前n個數值,而程式碼如下:

在工作表上執行此費波那契數列,輸出前12項。
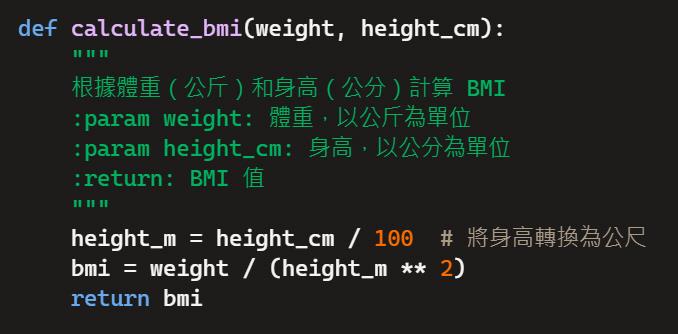
此外,透過各種不同的排序演算法,可以建構出各種不同的排序函數(Sorting Function),譬如:泡泡排序(Bubble Sort)、選擇排序(Selection Sort)、插入排序(Insertion Sort)、快速排序(Quick Sort)、合併排序(Merge Sort)、...等等。以下便是可以輸入2個參數的排序函數之虛擬碼(pseudocode)。第1個參數是尚未排序的數列,第二參數則是決定排序順序是由小到大或由大到小的布林值,當布林值為False時,可以對尚未排序的數列進行從小到大的排序,若布林值為True時,則是進行從大到小的排序。在此我們使用的排序演算法是泡泡排序法(Bubble sort),函數的輸出便是完成排序後的數列:

若是在Excel環境裡根據上述的虛擬碼,可以撰寫一個自訂函數來呈現泡泡排序法的運作,參考的VBA程式碼如下:
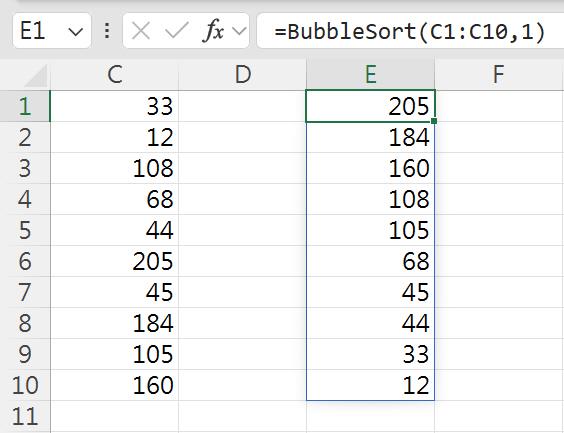
在工作表上執行此泡泡排序法的函數,第一個參數是尚未排序的資料範圍C1:C8;第二個參數是1,代表進行由大到小的排序。
此外,還有運用於將明文轉換為密文,以保護資訊安全的加密函數(Encryption Function);提供最短路徑演算法而應用於尋找從起點到終點的最短路徑函數(Shortest Path Function)等等,都是在電腦科學領域裡最為典型的運用。總之,電腦科學領域裡的函數運用真的是族繁不及備載。但由於這些電腦科學領域裡的函數議題並不在我們這一系列文章的範疇,有興趣的朋友就請自行爬文或求助AI幫幫忙囉!