函數(Function)是一個廣泛應用的關鍵概念,當我們談到函數時,其核心思維可以歸納為:「一種關係或機制,它根據輸入來產生輸出。」這種關係可以在不同的領域中以不同的方式呈現,不僅僅是在數學、物理、電腦科學、程式設計、應用軟體,乃至生活日常等領域均有廣泛應用,扮演著極其重要的角色。但不論哪一個領域,函數的基本概念是不變的,簡單來說,可以將函數理解為一種「對應關係」,可以將一個或多個輸入(稱為自變量)轉換為一個輸出(稱為因變量)。
1函數的特性與表達
我們可以在不同的領域中看到函數(Function)以不同的方式呈現,然而其基本概念始終不變。也就是函數的本質是映射(Mapping),即將一個輸入(Input)對應到一個輸出(Output)。一般來說,函數可以表達為:
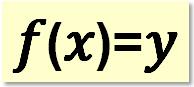
其中:
- f:表示函數的名稱
- x:輸入值(變數)
- y:輸出值(函數的結果)
- f(x):表示對輸入 x 套用函數後的結果
函數的概念
函數(或稱映射)具有多種特性,這些特性不僅對理解數學或相關理論非常重要,在各方面的應用也都發揮著關鍵作用。在此僅以易懂易學的解讀,摘要幾項函數的重要概念與特質:
1. 函數的核心概念:輸入與輸出
- 您可以把函數想像成一台機器或一個黑盒子。當您給它一些東西(輸入),它會根據內部的規則進行處理,然後給您一個結果(輸出)。

- 例如,在數學中,函數:
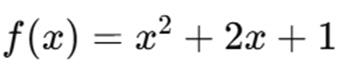
這便是一個簡單的多項式運算公式,表示:你輸入一個數 x,它會輸出 x 的平方加2倍的x最後再加1。譬如:輸入 3,輸出就是 16。藉由函數來表示特定的公式與運算。
2. 函數的規則性
- 函數的關鍵在於它的規則性。根據所輸入資料,函數都會按照固定的規則與邏輯來處理,並給出對應的輸出。例如:一個計算圓面積的函數 f(r)=π x r2 總是會根據半徑 r 來計算面積,不會因為其他因素而改變。
3. 函數的應用範圍
- 數學領域:函數用來描述變量之間的關係,例如線性函數、指數函數等。
- 電腦科學:函數是程式設計的基本單元,用來封裝一段可重複使用的程式碼,例如計算兩個數的和或處理字串。
- 物理學:函數用來描述自然現象中的規律,例如時間與速度的關係。
- 生活日常:函數的概念無處不在,例如食譜就是一種函數,食材是輸入,根據食譜裡的規則與邏輯的方式料理,輸出就是料理後的成品。
4. 函數的特性
- 重複的確定性:同的輸入,經過函數處理,一定會產生相同的輸出
- 獨立性:函數的輸出只依賴於輸入,不受外部因素影響。一個輸入只能對應到唯一的輸出,但不同的輸入可能會有相同的輸出。
- 組合性:函數可以互相組合,形成更複雜的功能。例如,一個函數的輸出可以作為另一個函數的輸入。
5. 生活日常的函數比喻
- 食譜:輸入食材,經過烹飪步驟(函數的規則與邏輯),輸出料理。
- 自動販賣機:投入錢幣(輸入),選擇飲料(規則與邏輯),輸出飲料。
- 翻譯機:輸入一種語言,輸出另一種語言。
總結
函數是一種將輸入轉換為輸出的規則或機制,它的核心在於「對應關係」。無論是在數學、電腦科學還是日常生活中,函數都提供了一種結構化的方式來描述和處理問題。理解函數的概念,可以幫助我們更清晰地分析問題並找到解決方案。