[R]讀取sav檔產生SPSS的KMO及Bartlett球形檢定

2019-09-16

1597
0
R語言

本文範例出處來自俞洪亮等人(2012)「商管研究資料分析：SPSS的應用」，使用R語言來模擬SPSS報表產生的結果。

quality.sav檔內容為高鐵設施的意見調查(共175件樣本)、其問項因子有五：

高鐵車站的動線標示清楚 (X1 )。
高鐵車廂乾淨清潔 (X2 )。
高鐵服務人員服裝賞心悅目 (X3 )。
高鐵服務人員的態度輕切 (X4 )。
乘坐高鐵非常舒適 (X5 )。 •

以李克特5點尺度為量度(5為非常滿意，1為非常不滿意)。

Bartlett球形檢定：呈現 χ 2 分佈，若變項間相關係數愈高，則所得 χ 2 值愈大，表示愈適合進行因素分析，卡方分佈對樣本大小相當敏銳，故實際分析時，很少呈現球形檢定接受虛無假設，即利用球形檢定法時，呈現資料不適宜進行因素分析結果的機率很低。巴特利球形檢定對樣本數量很敏感，只要樣本夠大，幾乎所有考驗都會達顯著水準，因此考驗結果只能作為參考，最好再參考其他不受樣本大小影響的方法，如Kaiser-Meyer-Olkin抽樣適切性量數（簡稱KMO，公式：相關係數平方和 / (相關係數平方和 + 淨相關係數平方和)）。

程式碼：

#install.packages("REdaS")
library(REdaS) #KMOS()及bart_spher()需要
sample <- read_spss("spss/quality.sav")
#Kaisar-Meyer-Olkin取樣適切性量數函式參考：https://www.rdocumentation.org/packages/REdaS/versions/0.9.0/topics/Kaiser-Meyer-Olkin-Statistics
kmo <- KMOS(sample)
print(paste0("Kaisar-Meyer-Olkin取樣適切性量數：", round(kmo[[7]], digits = 3)))
#巴特利球形檢定函式參考： https://www.rdocumentation.org/packages/REdaS/versions/0.9.3/topics/Bartlett-Sphericity
bart_spher(sample)

執行結果：

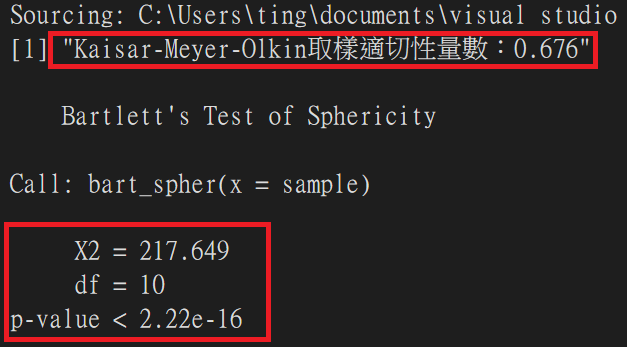
補充：KMO值的計算原始碼(參考：https://stat.ethz.ch/pipermail/r-help/2007-August/138049.html)

library(MASS) #ginv()需要
sample <- read_spss("spss/quality.sav")

# Kaiser-Meyer-Olkin計算方法(KMO) 
kmo = function(data) {
    X <- cor(as.matrix(data))
    iX <- ginv(X)
    S2 <- diag(diag((iX ^ -1)))
    AIS <- S2 %*% iX %*% S2
    Dai <- sqrt(diag(diag(AIS)))
    AIR <- ginv(Dai) %*% AIS %*% ginv(Dai)
    a <- apply((AIR - diag(diag(AIR))) ^ 2, 2, sum)
    b <- apply((X - diag(nrow(X))) ^ 2, 2, sum)
    MSA <- b / (b + a)
    AIR <- AIR - diag(nrow(AIR)) + diag(MSA)
    AA <- sum(a)
    BB <- sum(b)
    kmo <- BB / (AA + BB)
    return(round(kmo, digits = 3))
}

result <- kmo(sample)
print(paste0("Kaisar-Meyer-Olkin取樣適切性量數：", result))

執行結果：

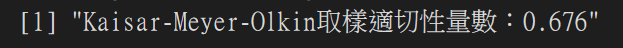
KMO value	Interpretation
>0.90	極佳(marvelous)
0.80~0.89	良好(meritorious)
0.70~0.79	中度(middling)
0.60~0.69	平庸(mediocre)
0.50~0.59	可悲(miserable)
<0.50	無法接受(unacceptable)

回首頁