Ryuichi's Arsenal

馬可夫鏈可以用一段時間的狀態移轉機率求穩態來去預測接下來傾向各狀態的機率為何。

但一般網路上提供的範例都是從機率矩陣開始，並不會清楚交代機率矩陣怎麼生出來的。

本次我們就用班級學生的考試成績(我們只挑Evan這位學生)，來去實作馬可夫鏈模擬預測學生接下來的考試成績會落在哪個區間。

我們準備4/1~4/30總共30天的資料(grade_20210401~20210430)，並將每天學生考試的成績紀錄下來。

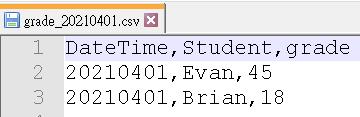
接著我們定義學生的分數屬於哪個區間，每位學生原則上每天考試的分數在0~100間。

我們定義80分以上(不含80分)Grade_H為高分區間(High)，60以下(不含60分)Grade_L為低分區間(Low)，介於60~80間的分數則為Grade_A中間區間(Average)。

#設定優劣等級threshold
high = 80
low = 60
#我們將讀進來的dataframe利用np.where將分數改為區間表示，0代表高分區間，1代表中間區間，2代表低分區間
full_data['grade'] = np.where(full_data['grade'] > high, 0, np.where(full_data['grade'] >= low, 1 ,2))

接著我們就會獲得學生在這30天內考試成績所屬區間的變化。

0,0,0,2,1,1,2,0,2,1,1,0,0,0,2,2,1,2,1,1……

接著我們建立一個3x3的二維陣列，將這些狀態的變化次數存進去。

grade = targetData['grade']
stat = np.zeros((dim, dim), dtype=float)
#stat = np.ones((dim, dim), dtype=float) -> 若你觀察的分數結果之歸類沒有 0 or 1 or 2 其中一種, 建議先將矩陣初始值設定成1, 避免馬可夫鏈無法計算
for i in range(len(targetData)-1):
    x = grade.values[i]
    y = grade.values[i+1]
    stat[x, y] += 1.0

以考試分數變化區間順序 0,0,0,2,1為例，代表0→0的次數為2次，0→2的次數為1次，2→1的次數為1次。

在stat二維陣列裡代表的就是stat[0,0]=2、stat[0,2]=1、stat[2,1]=1，我們可以用以下圖表呈現，分別是編號1~3的位置。

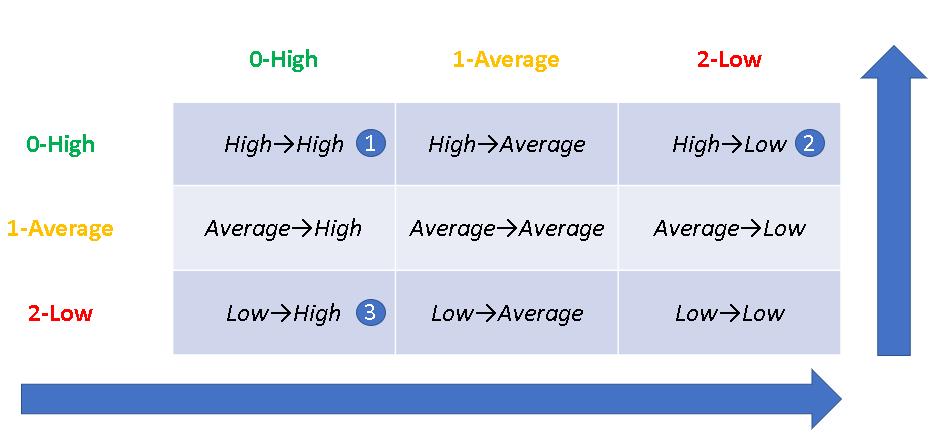
根據我手上的資料，以Evan的資料來看，我們使用他30天成績做預測，序列如下，2,0,1,0,0,2,2,1,2,2,0,2,1,1,0,0,2,2,2,2,2,1,1,2,1,2,2,2,2,2。

在表格內的次數呈現就如下圖。

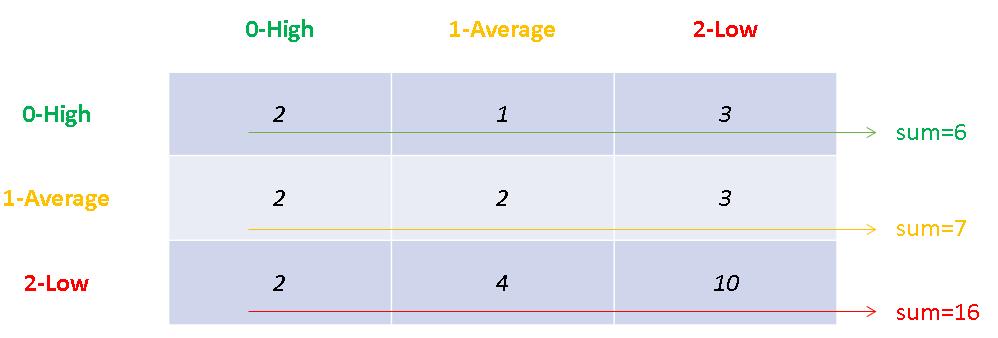
接著我們要算出每一個移轉狀態的初始機率，分別將九宮格內的數字除以該列的加總得到step=1的移轉機率。

summary = np.zeros(dim, dtype=float)
percent = np.zeros((dim, dim), dtype=float)
    for i in range(dim):
        summary[i] = np.sum(stat[i])
        for j in range(dim):
            if stat[i, j] != 0:
                percent[i ,j] = stat[i, j] / summary[i]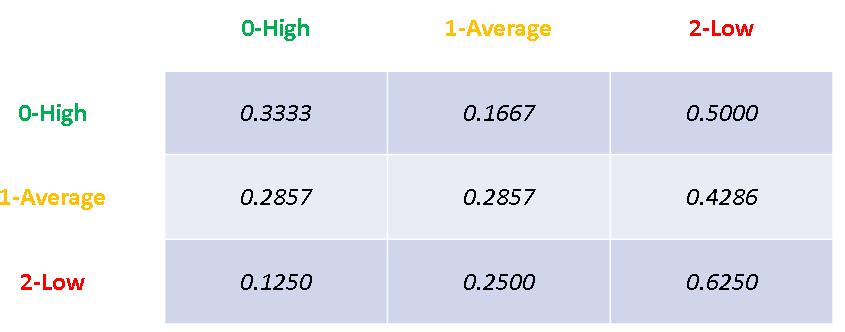

有了這個移轉機率矩陣後，我們便可以開始做矩陣相乘的動作求step=n時達到穩態。

如下圖，當N與N-1的矩陣完全相等時，程式停止即得穩態。

matrix = percent
for i in range(3,roundNum):
    matrix_1 = percent.dot(matrix)
    for j in range(0, len(matrix)):
        for k in range(0, len(matrix_1[j])):
            matrix_1[j][k] = '{0:.4f}'.format(matrix_1[j][k])
            
    if((matrix_1==matrix).all()):
        break #取得穩態, 收工
    matrix = matrix_1

#此段為預防機率矩陣為0時取該欄作為最大的防呆手段, 機率為0代表學生的分數狀態沒有落在該區間過。
Grade_H = [row[0] for row in matrix_1]
Grade_H = np.max(Grade_H)
Grade_A = [row[1] for row in matrix_1]
Grade_A = np.max(Grade_A)
Grade_L = [row[2] for row in matrix_1]
Grade_L = np.max(Grade_L)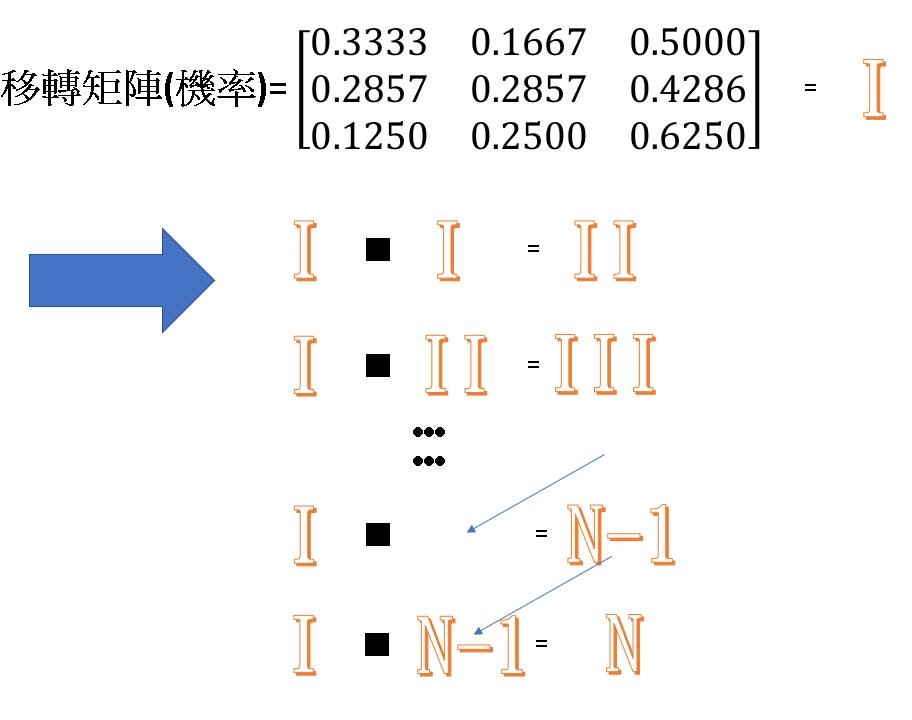

下表為Evan同學分別將前20日~前30日考試的成績經由馬可夫鏈計算預測成績落在各個區間的機率。

可以看到落在Low也就是低分區域的機率由4/20日預測的47.37%慢慢竄升到4/30日的55.17%。

這代表我們預測Evan同學接下來考試不及格(60分以下)的機率超過一半，Evan同學需要加油囉。

DateTime	Student	Grade-H	Grade-A	Grade-L
20210430	Evan	0.2069	0.2414	0.5517
20210429	Evan	0.2143	0.25	0.5357
20210428	Evan	0.2223	0.2593	0.5185
20210427	Evan	0.2308	0.2692	0.5
20210426	Evan	0.24	0.28	0.48
20210425	Evan	0.2581	0.2903	0.4516
20210424	Evan	0.2609	0.2609	0.4782
20210423	Evan	0.2857	0.2778	0.4365
20210422	Evan	0.3025	0.2353	0.4622
20210421	Evan	0.3	0.2	0.5
20210420	Evan	0.3158	0.2104	0.4737

完整程式如下：

# -*- coding: utf-8 -*-

"""
Created on Tue Sep 25 17:57:00 2021
@author: Ryuichi
"""
import os
import glob
import pandas as pd
import numpy as np
import datetime

#設定顯示所有欄位
pd.set_option('display.max_columns', None)
np.set_printoptions(precision=6, suppress=True, formatter={'float': '{: 0.4f}'.format})#float限定在小數點4位

#設定優劣等級threshold
high = 80
low = 60

#設定狀態維度(threshold分界數+1)
dim = 3

#設定資料最大天數日期
dateTimeString = '20210430'

#以dateTimeString為基底-(0~times-1)的資料
times = 11

#馬可夫鏈迭代次數
roundNum = 1000

#讀多個csv檔, merge成一個dataframe
def get_merged_csv(flist, **kwargs):
    return pd.concat([pd.read_csv(f, **kwargs) for f in flist], ignore_index=True)

#將所有要input的檔案整到一個資料夾下
path = 'D:/markovechain_pythonfile/inputFile'

#指定檔案的命名規則
fmask = os.path.join(path, 'grade_*.csv')

#讀取
full_data = get_merged_csv(glob.glob(fmask), index_col=None)#, usecols=['col1', 'col3']

#列印
#print(full_data.shape)

#取出要用的欄位
lst = ['DateTime','Student','grade']
full_data = full_data[full_data.columns.intersection(lst)]
full_data.info(verbose=True)#列出所有欄位的型態

print('------------------------------------')
#列印空值狀況
print(full_data.isnull().sum())
#踢掉有空值的資料
full_data.dropna(inplace=True)

#依據優劣等級threshold轉換數值為狀態
full_data['grade'] = np.where(full_data['grade'] > high, 0, np.where(full_data['grade'] >= low, 1 ,2))

#print(full_data.head())
data = {'DateTime':[],'Student':[],'Grade-H':[],'Grade-A':[],'Grade-L':[]}
predictResult = pd.DataFrame(data)
full_data = full_data[full_data['Student'].isin(['Evan'])]#只拿Evan同學作範例
#最大天數往前算前n日的狀況
for index in range(times):
    #進度條使用
    cnt = 1
    #取出指定日期前(含)的資料
    full_data_filter = full_data[full_data['DateTime'] <= int(dateTimeString)]
    #取出學生清單計算
    studentList = full_data_filter['Student'].unique().tolist()
    for student in studentList:
        #顯示進度
        print('*************************************************',dateTimeString+"["+str(cnt)+"/"+str(len(studentList))+"]")
        cnt = cnt +1
        targetData = full_data_filter[full_data_filter['Student'] == student]
        
        #依據日期排序
        targetData.sort_values('DateTime')
        grade = targetData['grade']
        stat = np.zeros((dim, dim), dtype=float)
        #stat = np.ones((dim, dim), dtype=float) -> 若你觀察的分數結果之歸類沒有 0 or 1 or 2 其中一種, 建議先將矩陣初始值設定成1, 避免馬可夫鏈無法計算
        ############################################
        #算出移轉次數矩陣
        for i in range(len(targetData)-1):
            x = grade.values[i]
            y = grade.values[i+1]
            stat[x, y] += 1.0
        
        #計算機率移轉矩陣
        summary = np.zeros(dim, dtype=float)
        percent = np.zeros((dim, dim), dtype=float)
        for i in range(dim):
            summary[i] = np.sum(stat[i])
            for j in range(dim):
                if stat[i, j] != 0:
                    percent[i ,j] = stat[i, j] / summary[i]
        ##########################################
        #矩陣相乘計算穩態
        matrix = percent
        for i in range(3,roundNum):
            matrix_1 = percent.dot(matrix)
            for j in range(0, len(matrix)):
                for k in range(0, len(matrix_1[j])):
                    matrix_1[j][k] = '{0:.4f}'.format(matrix_1[j][k])
                    
            if((matrix_1==matrix).all()):
                break
            matrix = matrix_1
        Grade_H = [row[0] for row in matrix_1]
        Grade_H = np.max(Grade_H)
        Grade_A = [row[1] for row in matrix_1]
        Grade_A = np.max(Grade_A)
        Grade_L = [row[2] for row in matrix_1]
        Grade_L = np.max(Grade_L)
        
        new_row = {'DateTime':str(dateTimeString),'Student':str(student),'Grade-H':str(Grade_H),'Grade-A':str(Grade_A),'Grade-L':str(Grade_L)}
        predictResult = predictResult.append(new_row, ignore_index=True)
        
    dateTimeObject = datetime.datetime.strptime(dateTimeString, '%Y%m%d')
    dateTimeObject = dateTimeObject - datetime.timedelta(days=1)
    dateTimeString = dateTimeObject.strftime("%Y%m%d")
predictResult.to_csv('./markovePredictResult_status.csv', index=False)#將預測結果儲存到檔案